1 前言

在儿童保健、临床疾病的诊断与治疗监测中，儿童青少年生长图表的应用越来越广泛。虽然我国在定期进行儿童生长发育调查和营养监测，但生长图表的制订研究尚不多见。

生长学（Auxology）数据通常为非正态分布。因此，Cole^[1]等曾提出了构建百分位数标准曲线的LMS方法，被一些国际卫生组织所采用^[2]。但LMS方法仅适用于呈偏态分布的数据，所以，Rigby et al. ^[3]报告了适用于偏态和峰态分布数据的Box-Cox幂指数分布模型（Box-Cox power exponential distribution，BCPE)，称为LMSP方法。2006年，世界卫生组织（WHO）统计专家组对30余种绘制生长曲线方法进行讨论，选择了BCPE模型来绘制生长曲线，提出了第一套世界卫生组织的儿童生长标准^[4]。

本文将应用BCPE分布模型，制订中国大中城市汉族儿童青少年的身高、体重、体重指数百分位数生长图表，为儿童期和青春期生长发育评价提供参考。

2 样本与方法

2.1样本

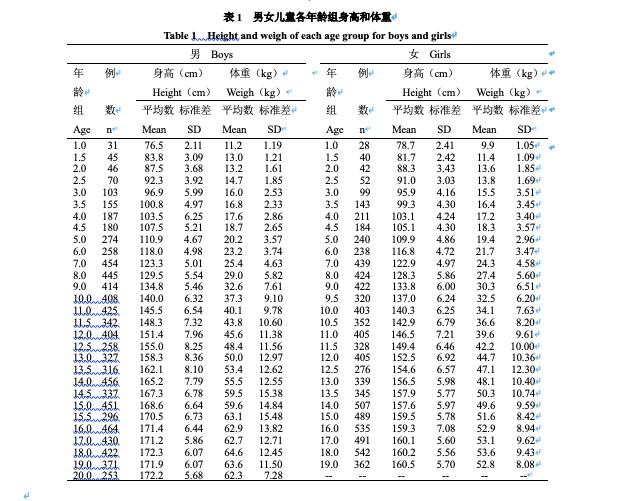
样本由上海市、广州市、温州市、大连市、石家庄市1-20岁的17401名汉族健康儿童所组成^[5]。选择市区管理规范的中小学校、幼儿园以及妇幼保健站为抽样点，按年龄分层整群抽样。3岁前在出生日前后7日内，其余在出生日前后15天之内调查取样，年龄组受试者例数、身高、体重数据见表1。

2.2 方法

采用BCPE分布模型，BCPE分布含有μ, σ, ν, τ四个解释变量参数，分别说明了数据分布的位置（中位数）、尺度（变异系数）、偏度（Box-Cox转换幂）和峰度（幂指数参数）。参数μ, σ, ν, τ的平滑均采用三次样条函数（cubic splines）。

在R程序软件中，应用广义的位置、尺度和形状相加模型^[6]（Generalized additive model for location, scale and shape，GAMLSS)计算解释变量函数，以衡量统计模型拟合优度标准的最小Akaike信息准则（Akaike Information Criterion, AIC）和GAIC(3) (Generalized AIC with penalty equal to 3)选择解释变量的自由度。BCPE模型的简化描述为BCPE[λ, df(μ), df(σ), df(υ), df(τ)]，λ为年龄的幂转换参数(x=age^λ)。

2.3 模型选择步骤

1、选择最佳df(μ), df(σ)组合：在正态分布（ν =1, τ =2）条件下，以发现超参数（find. Hyper()）函数初步选择df(μ), df(σ)，并选择总方差（global deviance，GD）最小时的λ₀为λ₁；然后以不同df(μ), df(σ)值拟合BCPE[λ₁, df(μ), df(σ), ν =1, τ =2]模型，以最小AIC和GAIC(3)分别选择df(μ), df(σ)组合。

2、选择最佳df(υ), df(τ)组合：分别选择出df(υ)，df(τ)；然后以不同的df(υ), df(τ)值拟合BCPE[λ₁, df(μ), df(σ), df(υ), df(τ)]模型，选择df(υ), df(τ)组合。

3、微调df(μ), df(σ)和λ₁：以不同df(μ), df(σ)值拟合BCPE[λ₁, df(μ), df(σ), df(υ), df(τ)]模型，选择分别有最小AIC和GAIC(3)的df(μ), df(σ)组合；再次选择最小GD时的λ₁为最终的λ。

4、确定最终的模型BCPE[λ, df(μ), df(σ), df(υ), df(τ)]。

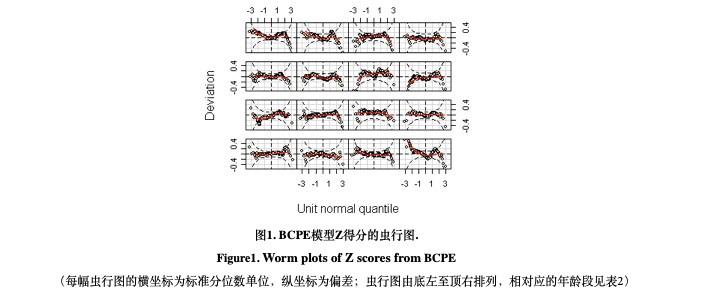
2.4 模型拟合优度的诊断与检验：

1、虫行图^[7]（Worm plots）：U形和S形的虫行轨迹分别说明模型拟合为偏态和峰态；三次多项式系数β1~β4分别超过0.10, 0.10, 0.05 和0.03的阈值视为模型违背。

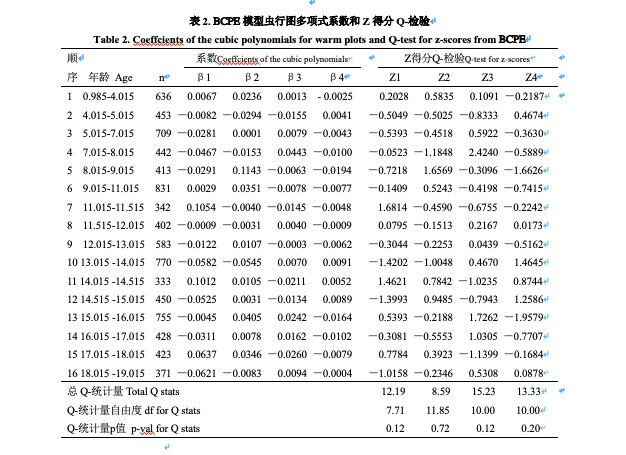
2、Q-检验：统计量Q1~Q4有显著性时分别说明模型参数μ, σ, ν和τ不适合；Z1~ Z4绝对值大于2时具有显著性，分别说明年龄组残数的平均数，标准差，偏度和峰度与正态分布不符。

3、结果

3.1 以男体重指数（BMI）为例的同类模型中的选择过程

依步骤的第1步选择出λ₁=0.9, df(μ)=6.29, df(σ)=5.3。但在检验中年龄组的虫行形状为U形，Z3、Z4大于2且总Q-统计量均具显著性（P=0.00）。进一步选择得到df(ν)=4和df(τ)=4。在微调步骤中，df(μ),和df(σ)无变化，但GD最小时的λ₁=0.70，则λ=0.70。最后模型为BCPE[x=age^0.7, df(μ)=6.29, df(σ)=5.3, df(ν)=4, df(τ)=4]。由图1可见，年龄组拟合数据的U形虫行轨迹消失，多项式系数低于阈值（表2），年龄组Z1~Z4均小于2（7-8岁组的Z3除外），总Q-统计量均无统计学显著性，p>0.05，得到了满意的拟合效果。

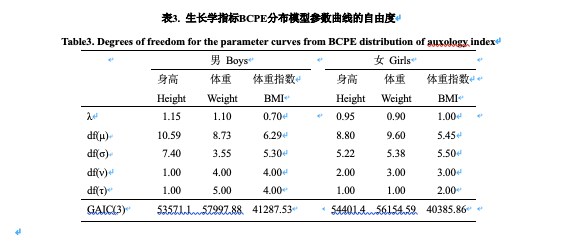
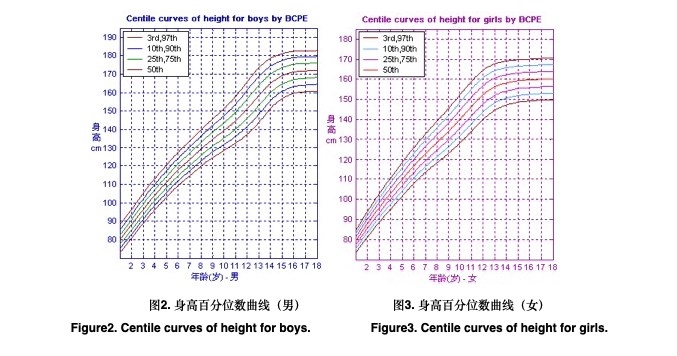
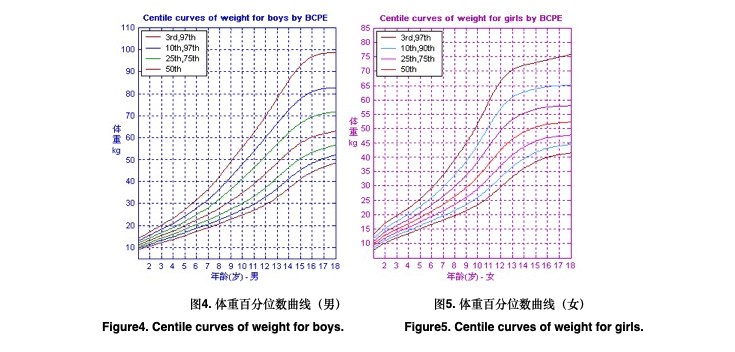
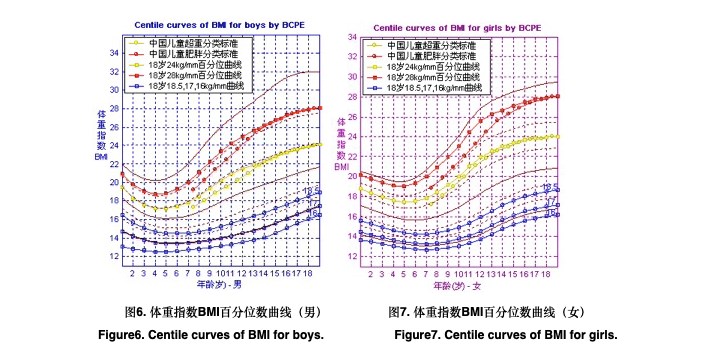
3.2 生长学指标的BCPE模型和百分位数生长图表

以上述过程，选择的生长学指标BCPE模型见表3；图2-图7为以BCPE分布模型拟合的百分位数曲线生长图表。为方便应用，在BMI生长图表中绘制出中国儿童超重、肥胖分类标准曲线^[8]，以及18岁时通过24kg/m²、28kg/m²界值点的BMI百分位曲线。同时，依据WHO成年人体瘦（thinness）的BMI分类标准^[9]，也绘出了18岁时通过18.5 kg/m²、17 kg/m²、16 kg/m²界值点的百分位数曲线。

4 讨论

BCCG分布模型（LMS方法）针对呈现偏态分布的数据，假设经过Box-Cox转换后数据近似正态分布；BCPE分布模型（LMSP方法）在LMS方法基础上增加了τ参数，使LMS方法广义化，不仅能够应用于偏态，而且可应用于峰态或同时呈现偏态和峰态分布的数据，增加了模型的灵活性，扩大了模型的应用范围，二者均为目前构建百分位数生长图表的较好方法。GAMLSS模型中含有多种不同类的模型，可以最简单的模型开始拟合百分位数生长曲线，通过虫行图和Q-检验逐步增加解释变量，使Box-Cox转换数据达到正态分布。本文在完成选择ν参数自由度这一步骤后，大部分年龄组Q-检验的Z4（峰度）仍然呈现统计学显著性，因此我们继续模型选择，并增加了选择最佳df(ν) 与df(τ)组合这一拟合步骤，以LMSP方法制订儿童青少年生长图表。

生长图表具有直观、简便，并可连续追踪被评价者纵向变化的优点。然而，国内生长图表的研制较少，其应用尚未普及。因而，我们以BCPE分布模型制订儿童青少年生长图表，以交流应用BCPE分布模型的经验。

【喜高科技】业内骨龄评价专家、专业骨龄研究科技机构及骨龄软件应用服务商！

热门文章推荐

手腕部桡、尺骨骺线消失作为推测18岁年龄的指征

青少年儿童年龄推断：骨发育长期趋势的影响

参考文献

[1] Cole T.J. The LMS method for constructing normalized growth standards. Euro J Clin Nutr, 1990, 44: 45-60.

[2] Cynthia L.O., Robert J. K., Katherine M. F., et al. Centers for Disease Control and Prevention 2000 Growth Charts for the United States: Improvements to the 1977 National Center for Health Statistics Version. Pediatrics, 2002, 109: 45-60.

[3] Rigby R.A., Stasinopoulos D.M. Smooth centile curves for skew and kurtotic data modeled using the Box-Cox power exponential distribution. Statistics in Medicine, 2004, 23: 3053–3076.

[4] Department of Nutrition for Health and Development. WHO Child Growth Standards: length/height-for-age, weight-for-age, weight-for-length, weight-forheight and body mass index-for-age : methods and development. ISBN 92 4 154693 X (NLM classification: WS 103) Geneva: World Health Organization.

[5] 张绍岩，刘丽娟，刘刚 等. 中国人手腕骨发育标准-中华05  I.TW₃-C RUS、TW₃-C Carpal、RUS-CHN方法 中国运动医学杂志 2006, 25(5): 6-13.

[6]Rigby RA, Stasinopoulos DM. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society - Series C - Applied Statistics, 2005, 54:507–544.

[7] van Buuren S, and Fredriks M. Worm plot: a simple diagnostic device for modeling growth reference curves. Statist Med, 2001, 20: 1259-1277.

[8] 中国肥胖问题工作组 中国学龄儿童青少年超重、肥胖筛查体重指数值分类标准 中华流行病学杂志 2004, 25(2): 97-102.

[9] WHO. Physical status: the use and interpretation of anthropometry. Geneva: WHO, 1995.